Liang-Barsky Line Clipping Algorithm,Algorithm

 

Liang-Barsky Line Clipping Algorithm:

Liang and Barsky have established an algorithm that uses floating-point arithmetic but finds the appropriate endpoints with at most four computations. This algorithm uses the parametric equations for a line and solves four inequalities to find the range of the parameter for which the line is in the viewport.

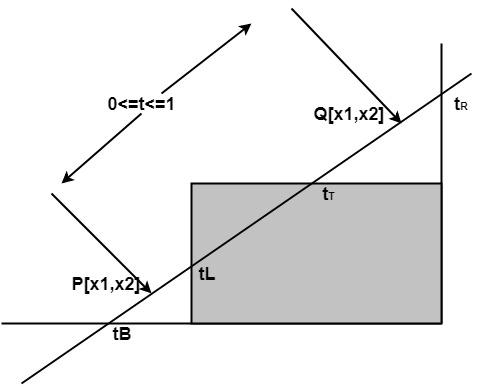
Let P(x1, y1), Q(x2, y2) is the line which we want to study. The parametric equation of the line segment from gives x-values and y-values for every point in terms of a parameter that ranges from 0 to 1. The equations are

x=x₁+(x₂-x₁ )*t=x₁+dx*t and y=y₁+(y₂-y₁ )*t=y₁+dy*t

We can see that when t = 0, the point computed is P(x1, y1); and when t = 1, the point computed is Q(x2, y2).

Algorithm of Liang-Barsky Line Clipping:

1. Set t_min=0 and t_max=1

2. Calculate the values t_L,t_R,t_T and t_B(tvalues).
      If tmin or tmax? ignore it and go to the next edge
      Otherwise classify the tvalue as entering or exiting value (using inner product to classify)
      If t is entering value set t_min=t if t is exiting value set t_max=t.

3. If t_min< t_max? then draw a line from (x1 + dx*t_min, y1 + dy*t_min) to (x1 + dx*t_max?, y1 + dy*t_max? )

4. If the line crosses over the window, you will see (x1 + dx*t_min, y1 + dy*t_min) and (x1 + dx*t_max? , y1 + dy*t_max?) are intersection between line and edge

The Liang-Barsky algorithm is a line clipping algorithm. This algorithm is more efficient than Cohen–Sutherland line clipping algorithm and can be extended to 3-Dimensional clipping. This algorithm is considered to be the faster parametric line-clipping algorithm. The following concepts are used in this clipping:

1. The parametric equation of the line.
2. The inequalities describing the range of the clipping window which is used to determine the intersections between the line and the clip window.

The parametric equation of a line can be given by,

X = x1 + t(x2-x1)
Y = y1 + t(y2-y1)

Where, t is between 0 and 1.

Then, writing the point-clipping conditions in the parametric form

xwmin <= x1 + t(x2-x1) <= xwmax
ywmin <= y1 + t(y2-y1) <= ywmax 

The above 4 inequalities can be expressed as,

tpk <= qk 

Where k = 1, 2, 3, 4 (correspond to the left, right, bottom, and top boundaries, respectively).

The p and q are defined as,

p1 = -(x2-x1),  q1 = x1 - xwmin (Left Boundary) 
p2 =  (x2-x1),  q2 = xwmax - x1 (Right Boundary)
p3 = -(y2-y1),  q3 = y1 - ywmin (Bottom Boundary) 
p4 =  (y2-y1),  q4 = ywmax - y1 (Top Boundary)  

When the line is parallel to a view window boundary, the p value for that boundary is zero.
When pk < 0, as t increase line goes from the outside to inside (entering).
When pk > 0, line goes from inside to outside (exiting).
When pk = 0 and qk < 0 then line is trivially invisible because it is outside view window.
When pk = 0 and qk > 0 then the line is inside the corresponding window boundary.

Using the following conditions, the position of line can be determined:

Condition	Position of line
pk = 0	parallel to the clipping boundaries
pk = 0 and qk < 0	completely outside the boundary
pk = 0 and qk >= 0	inside the parallel clipping boundary
pk < 0	line proceeds from outside to inside
pk > 0	line proceeds from inside to outside

Parameters t1 and t2 can be calculated that define the part of line that lies within the clip rectangle.
When,

1. pk < 0, maximum(0, qk/pk) is taken.
2. pk > 0, minimum(1, qk/pk) is taken.

If t1 > t2, the line is completely outside the clip window and it can be rejected. Otherwise, the endpoints of the clipped line are calculated from the two values of parameter t.

Algorithm –

1. Set tmin=0, tmax=1.
2. Calculate the values of t (t(left), t(right), t(top), t(bottom)),
   (i) If t < tmin ignore that and move to the next edge.
   (ii) else separate the t values as entering or exiting values using the inner product.
   (iii) If t is entering value, set tmin = t; if t is existing value, set tmax = t.
3. If tmin < tmax, draw a line from (x1 + tmin(x2-x1), y1 + tmin(y2-y1)) to (x1 + tmax(x2-x1), y1 + tmax(y2-y1))
4. If the line crosses over the window, (x1 + tmin(x2-x1), y1 + tmin(y2-y1)) and (x1 + tmax(x2-x1), y1 + tmax(y2-y1)) are the intersection point of line and edge.

This algorithm is presented in the following code. Line intersection parameters are initialised to the values t1 = 0 and t2 = 1.

#include"graphics.h" #define ROUND(a) ((int)(a+0.5)) int clipTest (float p,float q, float * tl, float * t2) { float r ; int retVal = TRUE;    //line entry point if (p < 0.0) {                r = q /p ;            // line portion is outside the clipping edge     if ( r > *t2 )                              retVal = FALSE;            else     if (r > *t1 )     *tl = r;  }    else    //line leaving point if (p>0.0) {                                  r = q/p ;            // line portion is outside          if ( r<*t1 )                                  retVal = FALSE;                    else i f (r<*t2)         *t2 = r; }    // p = 0, so line is parallel to this clipping edge  else        // Line is outside clipping edge  if (q<0.0)                                  retVal = FALSE;    return ( retVal ) ; }    void clipLine (dcPt winMin, dcPt winMax, wcPt2 pl , wcPt2 p2)     {  float t1 = 0.0, t2 = 1.0, dx = p2.x-p1.x, dy;     // inside test wrt left edge if(clipTest (-dx, p1.x - winMin.x, &t1, &t2))         // inside test wrt right edge  if(clipTest (dx, winMax.x - p1.x, &t1, &t2))     {                     dy = p2.y - p1.y;            // inside test wrt bottom edge      if(clipTest (-dy, p1.y - winMin.y, &t1, &t2))                // inside test wrt top edge          if(clipTest (dy, winMax.y - p1.y, &t1, &t2)) {                        if(t2 < 1.0) {             p2.x = p1.x + t2*dx;             p2.y = p1.y + t2*dy;         }                    if(t1 > 0.0) {             p1.x += t1*dx;             p1.y += t1*dy;         }                    lineDDA ( ROUND(p1.x), ROUND(p1.y), ROUND(p2.x), ROUND(p2.y) );                    } }    }