3-D Transformation

 3-D Transformation: In very general terms a 3D model is a mathematical representation of a physical entity that occupies space. In more practical terms, a 3D model is made of a description of its shape and a description of its color appearance.3-D Transformation is the process of manipulating the view of a three-D object with respect to its original position by modifying its physical attributes through various methods of transformation like Translation, Scaling, Rotation, Shear, etc. 

Properties of 3-D Transformation:

• Lines are preserved,
• Parallelism is preserved,
• Proportional distances are preserved.

One main categorization of a 3D object’s representation can be done by considering whether the surface or the volume of the object is represented:

Boundary-based: the surface of the 3D object is represented. This representation is also called b-rep. Polygon meshes, implicit surfaces, and parametric surfaces, which we will describe in the following, are common representations of this type

Volume-based: the volume of the 3D object is represented. Voxels and Constructive Solid Geometry (CSG) Are commonly used to represent volumetric data.

Types of Transformations:

1. Translation
2. Scaling
3. Rotation
4. Shear
5. Reflection

Translation: It is the process of changing the relative location of a 3-D object with respect to the original position by changing its coordinates. Translation transformation matrix in the 3-D image is shown as – Where Dx, Dy, Dz are the Translation distances, let a point in 3D space is P(x, y, z) over which we want to apply Translation Transformation operation and we are given with translation distance [Dx, Dy, Dz] So, new position of the point after applying translation operation would be – 

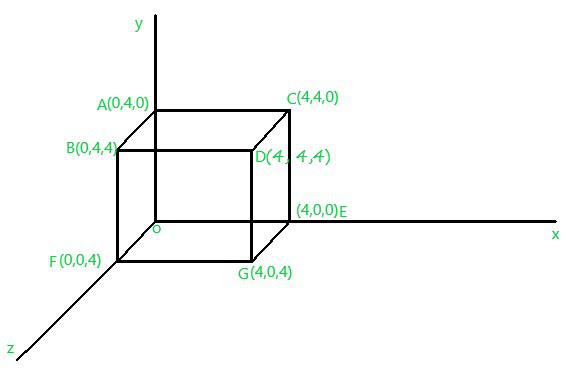
Problem: Perform translation transformation on the following figure where the given translation distances are Dx = 2, Dy = 4, Dz = 6. 

Solution: On applying Translation Transformation we get corresponding points –

Fig.1

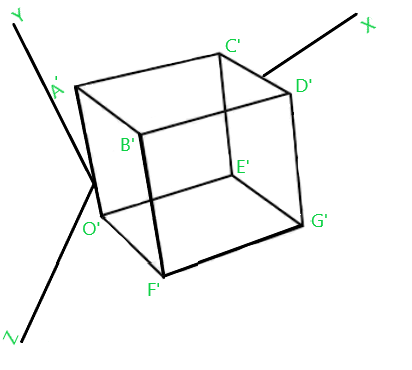
After performing translation transformation over the Fig.1, it will look like as below –

Fig.2

Translation

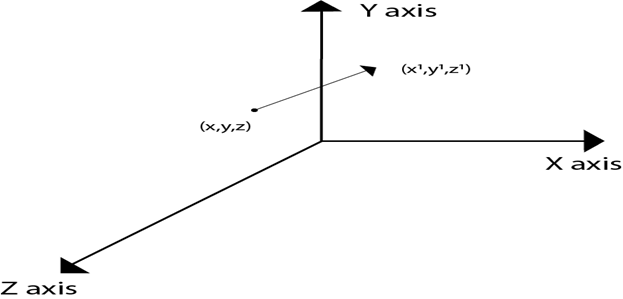
It is the movement of an object from one position to another position. Translation is done using translation vectors. There are three vectors in 3D instead of two. These vectors are in x, y, and z directions. Translation in the x-direction is represented using T_x. The translation is y-direction is represented using T_y. The translation in the z- direction is represented using T_z.

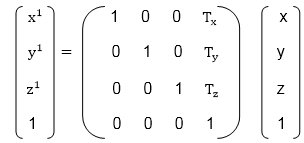
If P is a point having co-ordinates in three directions (x, y, z) is translated, then after translation its coordinates will be (x¹ y¹ z¹) after translation. T_x T_y T_z are translation vectors in x, y, and z directions respectively.

          x¹=x+ T_x
          y¹=y+T_y
          z¹=z+ T_z

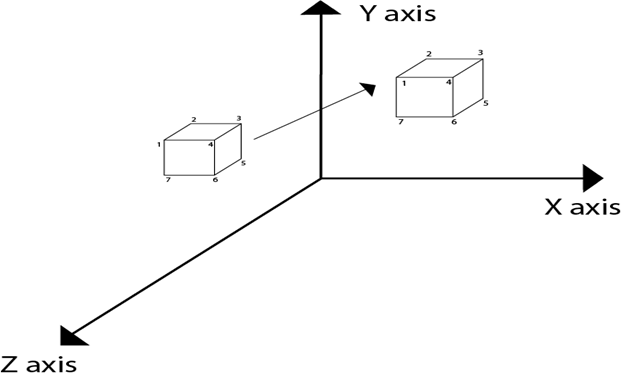
Three-dimensional transformations are performed by transforming each vertex of the object. If an object has five corners, then the translation will be accomplished by translating all five points to new locations. Following figure 1 shows the translation of point figure 2 shows the translation of the cube.

Matrix for translation

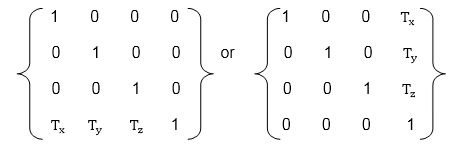
Matrix representation of point translation

Point shown in fig is (x, y, z). It become (x¹,y¹,z¹) after translation. T_x T_y T_z are translation vector.

Example: A point has coordinates in the x, y, z direction i.e., (5, 6, 7). The translation is done in the x-direction by 3 coordinate and y direction. Three coordinates and in the z- direction by two coordinates. Shift the object. Find coordinates of the new position.

Solution: Co-ordinate of the point are (5, 6, 7)
                 Translation vector in x direction = 3
                 Translation vector in y direction = 3
                 Translation vector in z direction = 2
                 Translation matrix is
                 

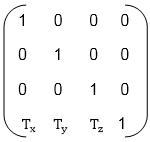
Multiply co-ordinates of point with translation matrix

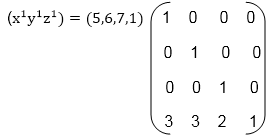
                 = [5+0+0+30+6+0+30+0+7+20+0+0+1] = [8991]

x becomes x¹=8
y becomes y¹=9
z becomes z¹=9