MidPoint Circle Algorithm,Algorithm,Program to draw a circle using Midpoint Algorithm

 

MidPoint Circle Algorithm

It is based on the following function for testing the spatial relationship between the arbitrary point (x, y) and a circle of radius r centered at the origin:

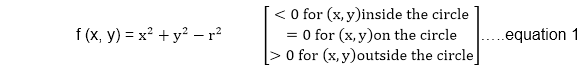
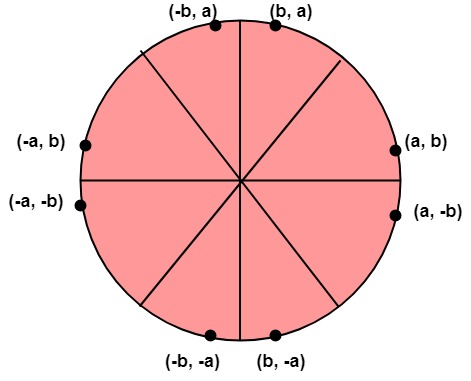
Now, consider the coordinates of the point halfway between pixel T and pixel S

This is called midpoint (x_i+1,y_i-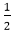) and we use it to define a decision parameter:

            P_i=f (x_i+1,y_i-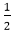) = (x_i+1)²+(y_i-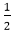)²-r² ...............equation 2If P_i is -ve ⟹midpoint is inside the circle and we choose pixel T

If P_i is+ve ⟹midpoint is outside the circle (or on the circle)and we choose pixel S.

The decision parameter for the next step is:

P_i+1=(x_i+1+1)²+(y_i+1-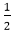)²- r²............equation 3

Since x_i+1=x_i+1, we have

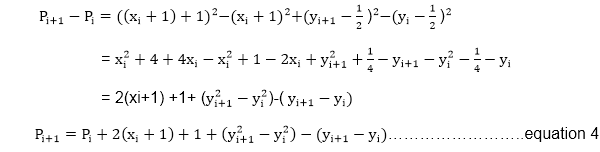
If pixel T is choosen ⟹P_i<0

We have y_i+1=y_i

If pixel S is choosen ⟹P_i≥0

We have y_i+1=y_i-1

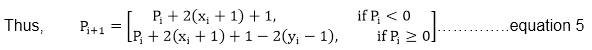
We can continue to simplify this in n terms of (x_i,y_i) and get

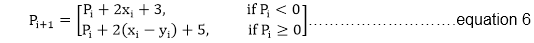
Now, initial value of P_i (0,r)from equation 2

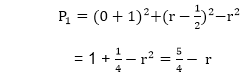
We can put 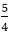≅1
∴r is an integer
So, P₁=1-r

Algorithm:

Step1: Put x =0, y =r in equation 2
            We have p=1-r

Step2: Repeat steps while x ≤ y
            Plot (x, y)
            If (p<0)
Then set p = p + 2x + 3
Else
            p = p + 2(x-y)+5
            y =y - 1 (end if)
            x =x+1 (end loop)

Step3: End

Program to draw a circle using Midpoint Algorithm:

1. #include <graphics.h>  
2. #include <stdlib.h>  
3. #include <math.h>  
4. #include <stdio.h>  
5. #include <conio.h>  
6. #include <iostream.h>  
7.   
8. class bresen  
9. {  
10.     float x, y,a, b, r, p;  
11.     public:  
12.     void get ();  
13.     void cal ();  
14. };  
15.     void main ()  
16.     {  
17.     bresen b;  
18.     b.get ();  
19.     b.cal ();  
20.     getch ();  
21.    }  
22.     Void bresen :: get ()  
23.    {  
24.     cout<<"ENTER CENTER AND RADIUS";  
25.      cout<< "ENTER (a, b)";  
26.     cin>>a>>b;  
27.     cout<<"ENTER r";  
28.     cin>>r;  
29. }  
30. void bresen ::cal ()  
31. {  
32.     /* request auto detection */  
33.     int gdriver = DETECT,gmode, errorcode;  
34.     int midx, midy, i;  
35.     /* initialize graphics and local variables */  
36.     initgraph (&gdriver, &gmode, " ");  
37.     /* read result of initialization */  
38.     errorcode = graphresult ();  
39.     if (errorcode ! = grOK)    /*an error occurred */  
40.     {  
41.         printf("Graphics error: %s \n", grapherrormsg (errorcode);  
42.         printf ("Press any key to halt:");  
43.         getch ();  
44.         exit (1); /* terminate with an error code */  
45.     }  
46.     x=0;  
47.     y=r;  
48.     putpixel (a, b+r, RED);  
49.     putpixel (a, b-r, RED);  
50.     putpixel (a-r, b, RED);  
51.     putpixel (a+r, b, RED);  
52.     p=5/4)-r;  
53.     while (x<=y)  
54.     {  
55.         If (p<0)  
56.         p+= (4*x)+6;  
57.         else  
58.         {  
59.             p+=(2*(x-y))+5;  
60.             y--;  
61.         }  
62.         x++;  
63.         putpixel (a+x, b+y, RED);  
64.         putpixel (a-x, b+y, RED);  
65.         putpixel (a+x, b-y, RED);  
66.         putpixel (a+x, b-y, RED);  
67.         putpixel (a+x, b+y, RED);  
68.         putpixel (a+x, b-y, RED);  
69.         putpixel (a-x, b+y, RED);  
70.         putpixel (a-x, b-y, RED);  
71.     }  
72. }  

Output:

---