DDA Algorithm,Symmetrical DDA,Program to implement DDA Line Drawing Algorithm,Advantage,Disadvantage

 

DDA Algorithm

DDA stands for Digital Differential Analyzer. It is an incremental method of scan conversion of line. In this method calculation is performed at each step but by using results of previous steps.

Suppose at step i, the pixels is (x_i,y_i)

The line of equation for step i
              y_i=mx_i+b......................equation 1

Next value will be
              y_i+1=m_xi+1+b.................equation 2
              m =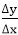
              y_i+1-y_i=∆y.......................equation 3
              y_i+1-x_i=∆x......................equation 4
              y_i+1=y_i+∆y
              ∆y=m∆x
              y_i+1=y_i+m∆x
              ∆x=∆y/m
              x_i+1=x_i+∆x
              x_i+1=x_i+∆y/mCase1: When |M|<1 then (assume that x₁2)

              x= x₁,y=y₁ set ∆x=1
              y_i+1=y_1+m,     x=x+1
              Until x = x₂

Case2: When |M|<1 then (assume that y₁2)
              x= x₁,y=y₁ set ∆y=1
              x_i+1=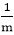,     y=y+1
              Until y → y₂

Advantage:

1. It is a faster method than method of using direct use of line equation.
2. This method does not use multiplication theorem.
3. It allows us to detect the change in the value of x and y ,so plotting of same point twice is not possible.
4. This method gives overflow indication when a point is repositioned.
5. It is an easy method because each step involves just two additions.

Disadvantage:

1. It involves floating point additions rounding off is done. Accumulations of round off error cause accumulation of error.
2. Rounding off operations and floating point operations consumes a lot of time.
3. It is more suitable for generating line using the software. But it is less suited for hardware implementation.

DDA Algorithm:

Step1: Start Algorithm

Step2: Declare x₁,y₁,x₂,y₂,dx,dy,x,y as integer variables.

Step3: Enter value of x₁,y₁,x₂,y₂.

Step4: Calculate dx = x₂-x₁

Step5: Calculate dy = y₂-y₁

Step6: If ABS (dx) > ABS (dy)
            Then step = abs (dx)
            Else

Step7: x_inc=dx/step
            y_inc=dy/step
            assign x = x₁
            assign y = y₁

Step8: Set pixel (x, y)

Step9: x = x + x_inc
            y = y + y_inc
            Set pixels (Round (x), Round (y))

Step10: Repeat step 9 until x = x₂

Step11: End AlgorithmExample: If a line is drawn from (2, 3) to (6, 15) with use of DDA. How many points will needed to generate such line?

Solution: P₁ (2,3)       P₁₁ (6,15)

                x₁=2
                y₁=3
                x₂= 6
                y₂=15
                dx = 6 - 2 = 4
                dy = 15 - 3 = 12
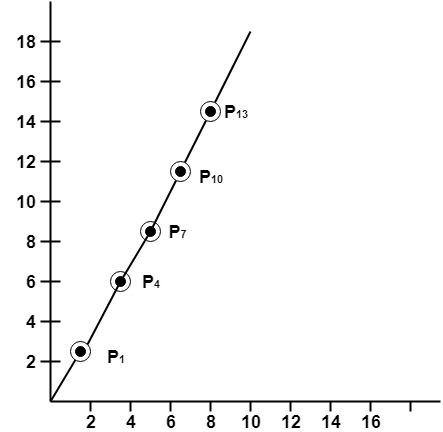
                m =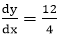 

For calculating next value of x takes x = x +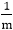 

Symmetrical DDA:

The Digital Differential Analyzer (DDA) generates lines from their differential equations. The equation of a straight line is

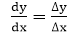
The DDA works on the principle that we simultaneously increment x and y by small steps proportional to the first derivatives of x and y. In this case of a straight line, the first derivatives are constant and are proportional to ∆x and ∆y . Therefore, we could generate a line by incrementing x and y by ϵ ∆x and ϵ ∆y, where ϵ is some small quantity. There are two ways to generate points

1. By rounding to the nearest integer after each incremental step, after rounding we display dots at the resultant x and y.

2. An alternative to rounding the use of arithmetic overflow: x and y are kept in registers that have two parts, integer and fractional. The incrementing values, which are both less than unity, are repeatedly added to the fractional parts and whenever the results overflows, the corresponding integer part is incremented. The integer parts of the x and y registers are used in plotting the line. In the case of the symmetrical DDA, we choose ε=2^-n,where 2^n-1≤max (|∆x|,|∆y|)<2^π

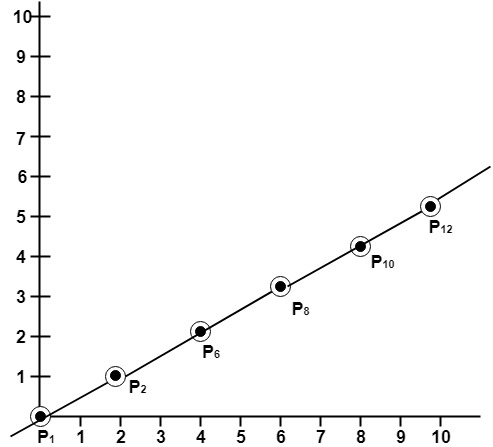
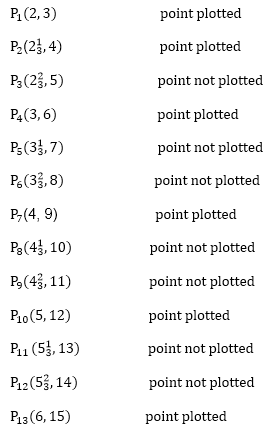
A line drawn with the symmetrical DDA is shown in fig:

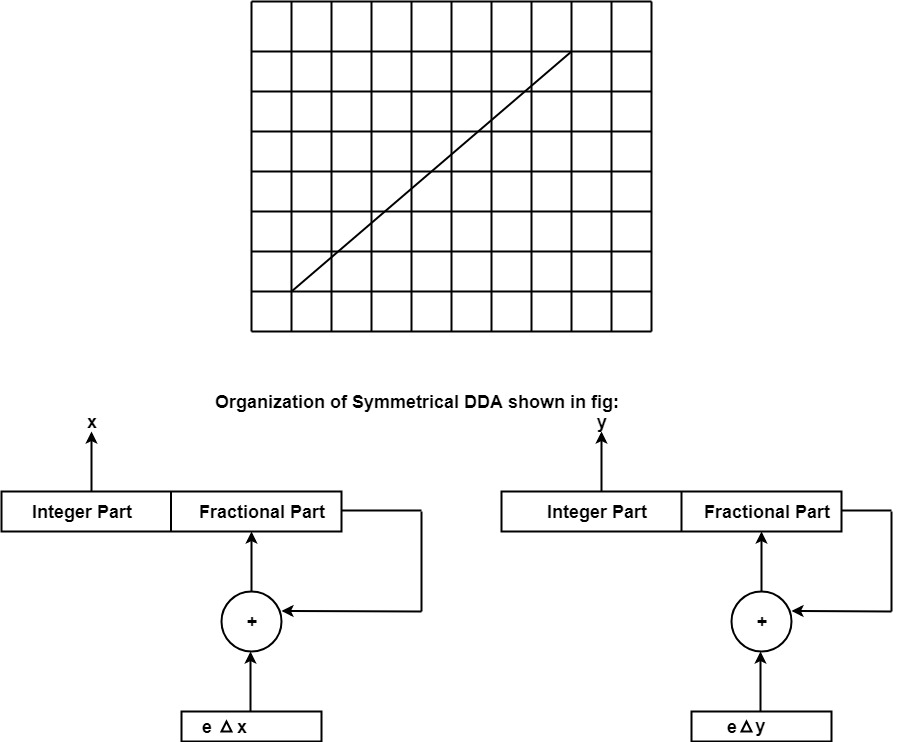
Example: If a line is drawn from (0, 0) to (10, 5) with a symmetrical DDA1. How many iterations are performed?

2. How many different points will be generated?

Solutions: Given: P¹ (0,0) P² (10,5)
                x¹=0
                y¹=0
                x²=10
                y²=5
                dx = 10 - 0 = 10
               dy = 5 - 0 = 0
                

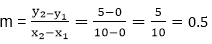
P¹ (0,0) will be considered starting points
P³ (1,0.5)                 point not plotted
P⁴ (2, 1)                 point plotted
P⁵ (3, 1.5)                 point not plotted
P⁶ (4,2)                 point plotted
P⁷ (5,2.5)                 point not plotted
P⁸ (6,3)                 point plotted
P⁹ (7,3.5)                 point not plotted
P¹⁰ (8, 4)                 point plotted
P¹¹ (9,4.5)                 point not plotted
P¹² (10,5)                 point plotted

Following Figure show line plotted using these points.

Program to implement DDA Line Drawing Algorithm:

1. #include<graphics.h>  
2. #include<conio.h>  
3. #include<stdio.h>  
4. void main()  
5. {  
6.     intgd = DETECT ,gm, i;  
7.     float x, y,dx,dy,steps;  
8.     int x0, x1, y0, y1;  
9.     initgraph(&gd, &gm, "C:\\TC\\BGI");  
10.     setbkcolor(WHITE);  
11.     x0 = 100 , y0 = 200, x1 = 500, y1 = 300;  
12.     dx = (float)(x1 - x0);  
13.     dy = (float)(y1 - y0);  
14.     if(dx>=dy)  
15.            {  
16.         steps = dx;  
17.     }  
18.     else  
19.            {  
20.         steps = dy;  
21.     }  
22.     dx = dx/steps;  
23.     dy = dy/steps;  
24.     x = x0;  
25.     y = y0;  
26.     i = 1;  
27.     while(i<= steps)  
28.     {  
29.         putpixel(x, y, RED);  
30.         x += dx;  
31.         y += dy;  
32.         i=i+1;  
33.     }  
34.     getch();  
    1. closegraph();  
    2. }  

    Output:

    

---