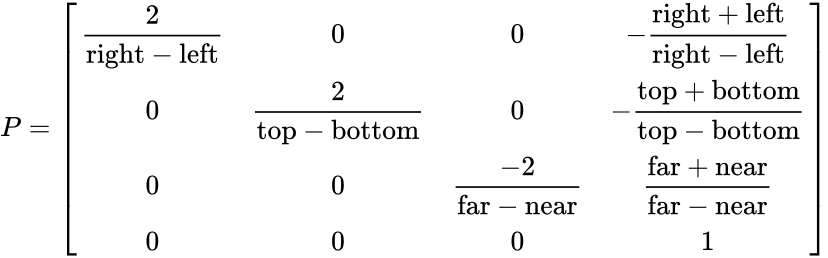Orthogonal projection
Parallel projection is further divided into two categories :
a) Orthographic Projection b) Oblique Projection
(a) Orthographic Projection : It is a kind of parallel projection where the projecting lines emerge parallelly from the object surface and incident perpendicularly at the projecting plane.
Orthographic Projection is of two categories :
(a).1. Multiview Projection : It is further divided into three categories –
(1) Top-View : In this projection, the rays that emerge from the top of the polygon surface are observed.

2) Side-View : It is another type of projection orthographic projection where the side view of the polygon surface is observed.

3) Front-view : In this orthographic projection front face view of the object is observed.

a.2) Axonometric : Axonometric projection is an orthographic projection, where the projection lines are perpendicular to the plane of projection, and the object is rotated around one or more of its axes to show multiple sides.
It is further divided into three categories :
(1) Isometric Projection : It is a method for visually representing three-dimensional objects in two-dimensional display in technical and engineering drawings. Here in this projection, the three coordinate axes appear equally foreshortened and the angle between any two of them is 120 degrees.

(2) Dimetric Projection : It is a kind of orthographic projection where the visualized object appears to have only two adjacent sides and angles are equal.

(3) Trimetric Projection : It is a kind of orthographic projection where the visualized object appears to have all the adjacent sides and angles unequal.

(b) Oblique Projection : It is a kind of parallel projection where projecting rays emerges parallelly from the surface of the polygon and incident at an angle other than 90 degrees on the plane.
It is of two kinds :
(b).1. Cavalier Projection : It is a kind of oblique projection where the projecting lines emerge parallelly from the object surface and incident at 45‘ rather than 90′ at the projecting plane. In this projection, the length of the reading axis is larger than the cabinet projection.

(b). 2. Cabinet Projection : It is similar to that cavalier projection but here the length of reading axes just half than the cavalier projection and the incident angle at the projecting plane is 63.4′ rather 45′.

Template:Views Orthographic projection (or orthogonal projection) is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. It is further divided into multiview orthographic projections and axonometric projections. A lens providing an orthographic projection is known as an (object-space) telecentric lens.
Geometry
A simple orthographic projection onto the plane can be defined by the following matrix:
For each point , the transformed point would be
Often, it is more useful to use homogeneous coordinates. The transformation above can be represented for homogeneous coordinates as
For each homogeneous vector , the transformed vector would be
In computer graphics, one of the most common matrices used for orthographic projection can be defined by a 6-tuple, (left, right, bottom, top, near, far), which defines the clipping planes. These planes form a box with the minimum corner at (left, bottom, near) and the maximum corner at (right, top, far).
The box is translated so that its center is at the origin, then it is scaled to the unit cube which is defined by having a minimum corner at and a maximum corner at .
The orthographic transform can be given by the following matrix:
which can be given as a scaling followed by a translation of the form
The inversion of the Projection Matrix, which can be used as the Unprojection Matrix is defined:
Multiview orthographic projections
With multiview orthographic projections, up to six pictures of an object are produced, with each projection plane parallel to one of the coordinate axes of the object. The views are positioned relative to each other according to either of two schemes: first-angle or third-angle projection. In each, the appearances of views may be thought of as being projected onto planes that form a 6-sided box around the object. Although six different sides can be drawn, usually three views of a drawing give enough information to make a 3D object. These views are known as front view, top view and end view.
Pictorials
Within orthographic projection there is the subcategory known as pictorials. Axonometric pictorials show an image of an object as viewed from a skew direction in order to reveal all three directions (axes) of space in a single picture.[3] Orthographic pictorial instrument drawings are often used to approximate graphical perspective projections, but there is attendant distortion in the approximation. Because pictorial projections inherently have this distortion, in the instrument drawing of pictorials, great liberties may then be taken for economy of effort and best effect. Orthographic pictorials rely on the technique of axonometric projection ("to measure along axes").
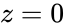 can be defined by the following matrix:
can be defined by the following matrix: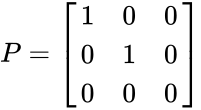
 , the transformed point would be
, the transformed point would be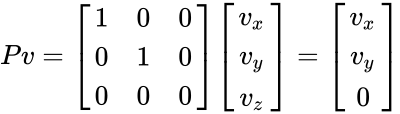
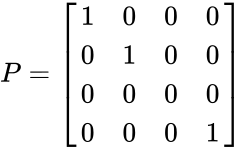
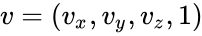 , the transformed vector would be
, the transformed vector would be
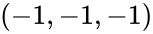 and a maximum corner at
and a maximum corner at 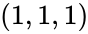 .
.